Bisektion
Bisektion er en metode fra numerisk analyse til at approksimering af rødder for funktioner således at hvis f er en kontinuerlig funktion.
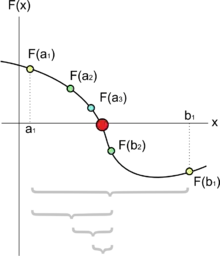
Illustration af bisektionsmetoden. Startintervallet er og følgende intervaller er .
![{\displaystyle [a_{1},b_{1}]}](../I/90b50cd52227fb045ffb69b5802b79b7b539e8d2.svg)
![{\displaystyle [a_{1},b_{2}],[a_{2},b_{2}],[a_{3},b_{2}]}](../I/06dac4fd5d233873038ac00311a273fa113b0146.svg)
Metoden
I metoden betragtes et interval hvor funktionen f skifter fortegn, hvorfor f et stedet i intervallet er nul, desuden skal funktion være kontinuerlig.
![{\displaystyle [a,b]}](../I/9c4b788fc5c637e26ee98b45f89a5c08c85f7935.svg)
Man finder et ny punkt i intervallet, , og hvis c selv er ikke et nulpunkt for funktionen så findes der to muligheder, har samme fortegn som eller . Nu laves et nyt interval ved at erstatte det tal af a og b hvor funktionen har samme fortegn i c med c, så man får intervallet eller . Proceduren forsættes på den måde indtil en tilstrækkelig nøjagtighed er opnået.
![{\displaystyle [a,c]}](../I/70b45aa26fb924cdd37786af1adcf5d58cfe15af.svg)
![{\displaystyle [c,b]}](../I/07f3f774df12e18b9f2bb94333ff320bbd2c308d.svg)
Se også
 | Spire Denne artikel om matematik er en spire som bør udbygges. Du er velkommen til at hjælpe Wikipedia ved at udvide den. |
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.