Indskreven cirkel

En indskreven cirkel er som oftest en cirkel i en trekant, hvis sider alle tangerer cirkelperiferien. Cirklens centrum befinder sig, hvor trekantens tre vinkelhalveringslinjer skærer hinanden.

Der er for få eller ingen kildehenvisninger i denne artikel, hvilket er et problem. Du kan hjælpe ved at angive troværdige kilder til de påstande, som fremføres i artiklen.

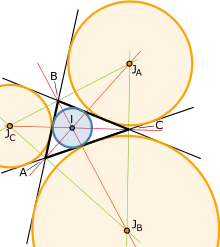
På denne skitse er den indskrevne cirkel blå, og vinkelhalvveringslinjerne går gennem dens centrum. På figuren er trekantens ydre røringscirkler farvet orange.

Er skæringspunktet ( S₁ ; S₂ ) først bestemt, er cirklens parametriske ligning givet ved:

${\displaystyle \left(S_{1}+R\cos t,S_{2}+R\sin t\right),R={\frac {c\cdot b\cdot \sin \left(A\right)}{a+b+c}}}$,

mens dens kartesiske ligning kan skrives på formen:

${\displaystyle \left(x-S_{1}\right)^{2}+\left(y-S_{2}\right)^{2}=R^{2}}$.

Bemærk, at radius ( R ) er lig med det dobbelte trekantsareal, divideret med trekantens omkreds.

Vedrørende trekantsarealet, se beviset for den såkaldte sinusrelation.