Keglestub
En keglestub er en kegle, hvor toppen er skåret af.
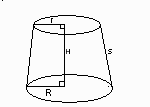
Arealet af den krumme overflade på en keglestub er givet ved
hvor:
- er radius i den store cirkulære endeflade.
- er radius i den lille cirkulære endeflade.
- er afstanden mellem de to cirkelperiferier.
kan udregnes vha. Pythagoras sætning (a²+b²=c²). a: keglestubbens højde, b: - og c: .
Altså:
Rumfanget (Volumen) af en keglestub er givet ved
hvor:
- er højden i figuren
- er radius i den store cirkulære endeflade.
- er radius i den lille cirkulære endeflade.
Bevis for rumfangs formel
Ovenstående formel kan findes ved at benytte reglen for udregning af volumen for omdrejnings legemer.
For en funktion som drejes 360˚ omkring x-aksen mellem punkterne og , kan man finde volumen af det frembragte omdrejnings legeme ved dette udtryk
For en keglestub gælder og det ønskede omdrejnings volumen findes med og .
Volumenet for en keglestub-skal med konstant tykkelse kan ud fra ovenstående vises at være
hvor:
- er skallens tykkelse målt parallelt med bunden og toppen.
- og er keglestubben udvendige mål
Hvis tykkelsen er målt vinkelret på skallens overflade skal erstattes med
hvor:
- er skallens tykkelse målt vinkelret på den skrå overflade.
Se også
- Pyramidestub
Eksterne henvisninger
| | Spire Denne artikel om geometri er en spire som bør udbygges. Du er velkommen til at hjælpe Wikipedia ved at udvide den. |