XY-modellen

XY-modellen er en relativt simpel model, der kan beskrive magnetisme i et material. Den består af et gitter, hvor der i hvert punkt er en enhedsvektor, kaldet et spin, der kan rotere i to dimensioner. Den er således en generalisering af Ising-modellen, hvor spinnene kun kan være +1 eller -1. Hvis de kan rotere i tre-dimensioner, kaldes modellen for Heisenberg-modellen. Alle tre er specialtilfælde er n-vektor-modellen, hvor spinnene kan rotere i ${\displaystyle n}$ dimensioner.

XY-modellen på et to-dimensionelt gitter. Farveskalaen angiver spinnnenes vinkel.

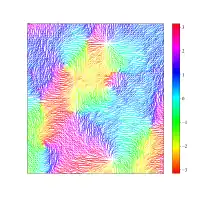
Modellen blev første gang publiceret i 1950 af Yoichiro Nambu,[1] mens en eksakt løsning for et én-dimensionelt gitter blev fundet vha. Jordan-Wigner-transformationen i 1961 af Elliott Lieb, Daniel Mattis og T. Schultz.[2]

I modellen er der ${\displaystyle N}$ gitterpunkter, hvor hvert punkt har et spin repræsenteret med enhedsvektoren ${\displaystyle {\vec {s}}_{i}}$. Spinnene interagerer med deres nærmeste naboer, hvor interaktionsenergien mellem to spin ${\displaystyle i}$ og ${\displaystyle j}$ er proportional med prikproduktet:

${\displaystyle {\mathcal {H}}_{ij}=-J{\vec {s}}_{i}\cdot {\vec {s}}_{j}}$

Hvis systemet udsættes for et ekstern magnetfelt ${\displaystyle {\vec {H}}}$, bidrager hvert spin yderligere med et prikprodukt med magnetfeltet:

${\displaystyle {\mathcal {H}}_{{\vec {H}},i}=-{\vec {H}}\cdot {\vec {s}}_{i}}$

De negative fortegn betyder, at det er energetisk fordelagtigt for et spin at pege i samme retning som dets naboer samt i samme retning som det eksterne magnetfelt. Energien for det samlede system er dermed:

${\displaystyle {\mathcal {H}}=-J\sum _{\langle i,j\rangle }{\vec {s}}_{i}\cdot {\vec {s}}_{j}-{\vec {H}}\cdot \sum _{i=1}^{N}{\vec {s}}_{i}}$

hvor den første sum er over alle nærmeste nabo-interaktioner, mens den anden er for hvert spin. Samlet har systemet desuden magnetiseringen ${\displaystyle {\vec {M}}}$, der er modellens ordensparameter:

På et gitter med to dimensioner eller højere optræder en faseovergang, men ved to dimensioner er overgangen den specielle Kosterlitz-Thouless-overgang. For denne overgang blev Nobelprisen i fysik givet i 2016 til John M. Kosterlitz og David J. Thouless.